The
atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons (except in the case of hydrogen-1, which is the only stable nuclide with no neutrons). The electrons of an atom are bound to the nucleus by the electromagnetic force. Likewise, a group of atoms can remain bound to each other by chemical bonds based on the same force, forming a molecule.
An atom containing an equal number of protons and electrons is
electrically neutral, otherwise it is positively or negatively charged
and is known as an ion. An atom is classified according to the number of protons and neutrons in its nucleus: the number of protons determines the chemical element, and the number of neutrons determines the isotope of the element.
 |
An illustration of the helium atom, depicting the nucleus (pink)
and the electron cloud
distribution (black). The nucleus (upper right)
in helium-4 is in
reality spherically symmetric and closely resembles
the electron cloud,
although for more complicated nuclei this is not
always the case. The
black bar is one angstrom (10−10 m or 100 pm). |
Chemical atoms, which in science now carry the simple name of "atom," are minuscule objects with diameters of a few tenths of a nanometer
and tiny masses proportional to the volume implied by these dimensions.
Atoms can only be observed individually using special instruments such
as the scanning tunneling microscope. Over 99.94% of an atom's mass is concentrated in the nucleus, with protons and neutrons having roughly equal mass. Each element has
at least one isotope with an unstable nucleus that can undergo radioactive decay. This can result in a transmutation that changes the number of protons or neutrons in a nucleus. Electrons that are bound to atoms possess a set of stable energy levels, or orbitals, and can undergo transitions between them by absorbing or emitting photons
that match the energy differences between the levels. The electrons
determine the chemical properties of an element, and strongly influence
an atom's magnetic properties. The principles of quantum mechanics have been successfully used to model the observed properties of the atom.
Etymology
The name atom comes from the Greek ἄτομος (
atomos, "indivisible") from
ἀ- (
a-, "not") and
τέμνω (
temnō, "I cut"), which means uncuttable, or indivisible, something that cannot be divided further. The concept of an atom as an indivisible component of matter was first proposed by early Indian and Greek philosophers. In the 18
th and 19
th centuries, chemists
provided a physical basis for this idea by showing that certain
substances could not be further broken down by chemical methods, and
they applied the ancient philosophical name of
atom to the chemical entity. During the late 19
th and early 20
th centuries, physicists
discovered subatomic components and structure inside the atom, thereby
demonstrating that the chemical "atom" was divisible and that the name
might not be appropriate.
However, it was retained. This has led to some debate about whether the
ancient philosophers, who intended to refer to fundamental individual
objects with their concept of "atoms," were referring to modern chemical
atoms, or something more like indivisible subatomic particles such as leptons or quarks, or even some more fundamental particle that has yet to be discovered.
History
Atomism
The concept that matter is composed of discrete units and cannot be divided into arbitrarily tiny quantities has been around for millennia, but these ideas were founded in abstract, philosophical reasoning rather than experimentation and empirical observation.
The nature of atoms in philosophy varied considerably over time and
between cultures and schools, and often had spiritual elements.
Nevertheless, the basic idea of the atom was adopted by scientists
thousands of years later because it elegantly explained new discoveries
in the field of chemistry.
References to the concept of atoms date back to ancient Greece and India. In India, the Ājīvika, Jain, and Cārvāka schools of atomism may date back to the 6th century BCE. The Nyaya and Vaisheshika schools later developed theories on how atoms combined into more complex objects. In the West, the references to atoms emerged in the 5th century BCE with Leucippus, whose student, Democritus, systematized his views. In approximately 450 BCE, Democritus coined the term
átomos (Greek:
ἄτομος), which means "uncuttable" or "the smallest indivisible particle of matter". Although the Indian and Greek concepts of the atom were based purely on philosophy, modern science has retained the name coined by Democritus.
Corpuscularianism is the postulate, expounded in the 13th-century by the alchemist Pseudo-Geber (Geber), sometimes identified with Paul of Taranto, that all physical bodies possess an inner and outer layer of minute particles or corpuscles.
Corpuscularianism is similar to the theory of atomism, except that
where atoms were supposed to be indivisible, corpuscles could in
principle be divided. In this manner, for example, it was theorized that
mercury could penetrate into metals and modify their inner structure. Corpuscularianism stayed a dominant theory over the next several hundred years.
In 1661, natural philosopher Robert Boyle published
The Sceptical Chymist in which he argued that matter was composed of various combinations of different "corpuscules" or atoms, rather than the classical elements of air, earth, fire and water. During the 1670s corpuscularianism was used by Isaac Newton in his development of the corpuscular theory of light.
Origin of scientific theory
 |
Various atoms and molecules as depicted in John Dalton's
A New System of Chemical Philosophy (1808), one of the earliest scientific works on atomic theory |
Further progress in the understanding of atoms did not occur until the science of chemistry began to develop. In 1789, French nobleman and scientific researcher Antoine Lavoisier discovered the law of conservation of mass and defined an element as a basic substance that could not be further broken down by the methods of chemistry.
In 1805, English instructor and natural philosopher John Dalton used the concept of atoms to explain why elements always react in ratios of small whole numbers (the law of multiple proportions)
and why certain gases dissolved better in water than others. He
proposed that each element consists of atoms of a single, unique type,
and that these atoms can join together to form chemical compounds. Dalton is considered the originator of modern atomic theory.
Dalton's atomic hypothesis did not specify the size of atoms. Common
sense indicated they must be very small, but nobody knew how small.
Therefore it was a major landmark when in 1865 Johann Josef Loschmidt measured the size of the molecules that make up air.
An additional line of reasoning in support of particle theory (and by extension atomic theory) began in 1827 when botanist Robert Brown used a microscope to look at dust grains floating in water and discovered that they moved about erratically—a phenomenon that became known as "Brownian motion". J. Desaulx suggested in 1877 that the phenomenon was caused by the thermal motion of water molecules, and in 1905 Albert Einstein produced the first mathematical analysis of the motion. French physicist Jean Perrin
used Einstein's work to experimentally determine the mass and
dimensions of atoms, thereby conclusively verifying Dalton's atomic
theory.
 |
| Mendeleev's first periodic table (1869) |
In 1869, building upon earlier discoveries by such scientists as Lavoisier, Dmitri Mendeleev published the first functional periodic table. The table itself is a visual representation of the periodic law, which states that certain chemical properties of elements repeat
periodically when arranged by atomic number.
Subcomponents and quantum theory
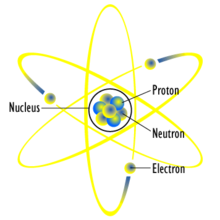 |
| A generic atomic planetary model, or the Rutherford model |
The physicist J. J. Thomson, through his work on cathode rays
in 1897, discovered the electron, and concluded that they were a
component of every atom. Thus he overturned the belief that atoms are
the indivisible, ultimate particles of matter.
Thomson postulated that the low mass, negatively charged electrons were
distributed throughout the atom, possibly rotating in rings, with their
charge balanced by the presence of a uniform sea of positive charge.
This later became known as the plum pudding model.
In 1909, Hans Geiger and Ernest Marsden, under the direction of physicist Ernest Rutherford, bombarded a sheet of gold foil with alpha rays—by
then known to be positively charged helium atoms—and discovered that a
small percentage of these particles were deflected through much larger
angles than was predicted using Thomson's proposal. Rutherford
interpreted the gold foil experiment
as suggesting that the positive charge of a heavy gold atom and most of
its mass was concentrated in a nucleus at the center of the atom—the Rutherford model.
While experimenting with the products of radioactive decay, in 1913 radiochemist Frederick Soddy discovered that there appeared to be more than one type of atom at each position on the periodic table. The term isotope was coined by Margaret Todd
as a suitable name for different atoms that belong to the same element.
J.J. Thomson created a technique for separating atom types through his
work on ionized gases, which subsequently led to the discovery of stable isotopes.
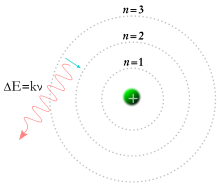 |
A Bohr model of the hydrogen atom, showing an electron jumping
between fixed orbits and emitting a photon of energy with a specific frequency |
Meanwhile, in 1913, physicist Niels Bohr
suggested that the electrons were confined into clearly defined,
quantized orbits, and could jump between these, but could not freely
spiral inward or outward in intermediate states.
An electron must absorb or emit specific amounts of energy to transition between these fixed orbits. When the light from a heated material was passed through a prism, it produced a multi-colored spectrum. The appearance of fixed lines in this spectrum was successfully explained by these orbital transitions.
Later in the same year Henry Moseley provided additional experimental evidence in favor of Niels Bohr's theory. These results refined Ernest Rutherford's and Antonius Van den Broek's model, which proposed that the atom contains in its nucleus a number of positive nuclear charges that is equal to its (atomic) number in the periodic table. Until these experiments, atomic number
was not known to be a physical and experimental quantity. That it is
equal to the atomic nuclear charge remains the accepted atomic model
today.
Chemical bonds between atoms were now explained, by Gilbert Newton Lewis in 1916, as the interactions between their constituent electrons. As the chemical properties of the elements were known to largely repeat themselves according to the periodic law, in 1919 the American chemist Irving Langmuir
suggested that this could be explained if the electrons in an atom were
connected or clustered in some manner. Groups of electrons were thought
to occupy a set of electron shells about the nucleus.
The Stern–Gerlach experiment
of 1922 provided further evidence of the quantum nature of the atom.
When a beam of silver atoms was passed through a specially shaped
magnetic field, the beam was split based on the direction of an atom's
angular momentum, or spin. As this direction is random, the beam could
be expected to spread into a line. Instead, the beam was split into two
parts, depending on whether the atomic spin was oriented up or down.
In 1924, Louis de Broglie proposed that all particles behave to an extent like waves. In 1926, Erwin Schrödinger used this idea to develop a mathematical model of the atom that described the electrons as three-dimensional waveforms
rather than point particles. A consequence of using waveforms to
describe particles is that it is mathematically impossible to obtain
precise values for both the position and momentum of a particle at the same time; this became known as the uncertainty principle, formulated by Werner Heisenberg
in 1926. In this concept, for a given accuracy in measuring a position
one could only obtain a range of probable values for momentum, and vice
versa. This model was able to explain observations of atomic behavior
that previous models could not, such as certain structural and spectral patterns of atoms larger than hydrogen. Thus, the planetary model of the atom was discarded in favor of one that described atomic orbital zones around the nucleus where a given electron is most likely to be observed.
 |
| Schematic diagram of a simple mass spectrometer |
The development of the mass spectrometer
allowed the exact mass of atoms to be measured. The device uses a
magnet to bend the trajectory of a beam of ions, and the amount of
deflection is determined by the ratio of an atom's mass to its charge.
The chemist Francis William Aston used this instrument to show that isotopes had different masses. The atomic mass of these isotopes varied by integer amounts, called the whole number rule. The explanation for these different isotopes awaited the discovery of the neutron, a neutral-charged particle with a mass similar to the proton, by the physicist James Chadwick
in 1932. Isotopes were then explained as elements with the same number
of protons, but different numbers of neutrons within the nucleus.
Fission, high-energy physics and condensed matter
In 1938, the German chemist Otto Hahn, a student of Rutherford, directed neutrons onto uranium atoms expecting to get transuranium elements. Instead, his chemical experiments showed barium as a product. A year later, Lise Meitner and her nephew Otto Frisch verified that Hahn's result were the first experimental
nuclear fission. In 1944, Hahn received the Nobel prize in chemistry. Despite Hahn's efforts, the contributions of Meitner and Frisch were not recognized.
In the 1950s, the development of improved particle accelerators and particle detectors allowed scientists to study the impacts of atoms moving at high energies. Neutrons and protons were found to be hadrons, or composites of smaller particles called quarks. The standard model of particle physics
was developed that so far has successfully explained the properties of
the nucleus in terms of these sub-atomic particles and the forces that
govern their interactions.
 , the fraction
, the fraction  . Therefore, multiplying by
. Therefore, multiplying by  is equivalent to multiplying by one, and any number multiplied by one
has the same value as the original number. By way of an example, start
with the fraction
is equivalent to multiplying by one, and any number multiplied by one
has the same value as the original number. By way of an example, start
with the fraction 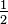 .
.