Equivalent fractions
Multiplying the numerator and denominator of a fraction by the same (non-zero) number results in a fraction that is equivalent to the original fraction. This is true because for any non-zero number , the fraction
, the fraction  . Therefore, multiplying by
. Therefore, multiplying by  is equivalent to multiplying by one, and any number multiplied by one
has the same value as the original number. By way of an example, start
with the fraction
is equivalent to multiplying by one, and any number multiplied by one
has the same value as the original number. By way of an example, start
with the fraction 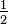 .
.When the numerator and denominator are both multiplied by 2, the result is
 , which has the same value (0.5) as
, which has the same value (0.5) as 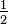 . To picture this visually, imagine cutting a cake into four pieces; two of the pieces together (
. To picture this visually, imagine cutting a cake into four pieces; two of the pieces together ( ) make up half the cake (
) make up half the cake (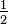 ).
).Dividing the numerator and denominator of a fraction by the same non-zero number will also yield an equivalent fraction. This is called reducing or simplifying the fraction. A simple fraction in which the numerator and denominator are coprime [that is, the only positive integer that goes into both the numerator and denominator evenly is 1) is said to be irreducible, in lowest terms, or in simplest terms. For example,
 is not in lowest terms because both 3 and 9 can be exactly divided by 3. In contrast,
is not in lowest terms because both 3 and 9 can be exactly divided by 3. In contrast,  is in lowest terms—the only positive integer that goes into both 3 and 8 evenly is 1.
is in lowest terms—the only positive integer that goes into both 3 and 8 evenly is 1.Using these rules, we can show that
 =
= 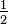 =
=  =
= 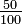 .
.A common fraction can be reduced to lowest terms by dividing both the numerator and denominator by their greatest common divisor. For example, as the greatest common divisor of 63 and 462 is 21, the fraction
 can be reduced to lowest terms by dividing the numerator and denominator by 21:
can be reduced to lowest terms by dividing the numerator and denominator by 21:Comparing fractions
Comparing fractions with the same denominator only requires comparing the numerators. because 3>2.
because 3>2.
One way to compare fractions with different numerators and denominators is to find a common denominator. To compare
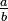 and
and 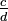 , these are converted to
, these are converted to 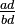 and
and  . Then bd is a common denominator and the numerators ad and bc can be compared.
. Then bd is a common denominator and the numerators ad and bc can be compared. ?
? 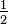 gives
gives 
 ?
? 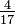
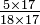 ?
? 
 .
.Also note that every negative number, including negative fractions, is less than zero, and every positive number, including positive fractions, is greater than zero, so every negative fraction is less than any positive fraction.
Addition
The first rule of addition is that only like quantities can be added; for example, various quantities of quarters. Unlike quantities, such as adding thirds to quarters, must first be converted to like quantities as described below: Imagine a pocket containing two quarters, and another pocket containing three quarters; in total, there are five quarters. Since four quarters is equivalent to one (dollar), this can be represented as follows: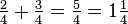 .
.
 |
If 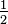 of a cake is to be added to of a cake is to be added to  of a cake, the pieces need to be of a cake, the pieces need to be converted into comparable quantities, such as cake-eighths or cake-quarters. |
Adding unlike quantities
To add fractions containing unlike quantities (e.g. quarters and thirds), it is necessary to convert all amounts to like quantities. It is easy to work out the chosen type of fraction to convert to; simply multiply together the two denominators (bottom number) of each fraction.For adding quarters to thirds, both types of fraction are converted to twelfths, thus:
 .
.Consider adding the following two quantities:
 into twelfths by multiplying both the numerator and denominator by three:
into twelfths by multiplying both the numerator and denominator by three: 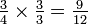 . Since
. Since  equals 1, multiplication by
equals 1, multiplication by  does not change the value of the fraction.
does not change the value of the fraction.Second, convert
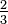 into twelfths by multiplying both the numerator and denominator by four:
into twelfths by multiplying both the numerator and denominator by four:  .
.Now it can be seen that:
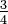 and
and  the denominator 48 can be used (the product of 4 and 12), but the smaller denominator 12 may also be used, being the least common multiple of 4 and 12.
the denominator 48 can be used (the product of 4 and 12), but the smaller denominator 12 may also be used, being the least common multiple of 4 and 12.Subtraction
The process for subtracting fractions is, in essence, the same as that of adding them: find a common denominator, and change each fraction to an equivalent fraction with the chosen common denominator. The resulting fraction will have that denominator, and its numerator will be the result of subtracting the numerators of the original fractions. For instance,Multiplication
Multiplying a fraction by another fraction
To multiply fractions, multiply the numerators and multiply the denominators. Thus:A short cut for multiplying fractions is called "cancellation". In effect, we reduce the answer to lowest terms during multiplication. For example:
Multiplying a fraction by a whole number
Place the whole number over one and multiply.Mixed numbers
When multiplying mixed numbers, it's best to convert the mixed number into an improper fraction. For example: is the same as
is the same as  , making 11 quarters in total (because 2 cakes, each split into quarters makes 8 quarters total) and 33 quarters is
, making 11 quarters in total (because 2 cakes, each split into quarters makes 8 quarters total) and 33 quarters is  , since 8 cakes, each made of quarters, is 32 quarters in total.
, since 8 cakes, each made of quarters, is 32 quarters in total.Division
To divide a fraction by a whole number, you may either divide the numerator by the number, if it goes evenly into the numerator, or multiply the denominator by the number. For example, equals
equals  and also equals
and also equals 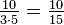 , which reduces to
, which reduces to  . To divide a number by a fraction, multiply that number by the reciprocal of that fraction. Thus,
. To divide a number by a fraction, multiply that number by the reciprocal of that fraction. Thus,  .
.Converting between decimals and fractions
To change a common fraction to a decimal, divide the denominator into the numerator. Round the answer to the desired accuracy. For example, to change 1/4 to a decimal, divide 4 into 1.00, to obtain 0.25. To change 1/3 to a decimal, divide 3 into 1.0000..., and stop when the desired accuracy is obtained. Note that 1/4 can be written exactly with two decimal digits, while 1/3 cannot be written exactly with any finite number of decimal digits.To change a decimal to a fraction, write in the denominator a 1 followed by as many zeroes as there are digits to the right of the decimal point, and write in the numerator all the digits in the original decimal, omitting the decimal point. Thus 12.3456 = 123456/10000.
Converting repeating decimals to fractions
The preferred way to indicate a repeating decimal is to place a bar over the digits that repeat, for example 0.789 = 0.789789789… For repeating patterns where the repeating pattern begins immediately after the decimal point, a simple division of the pattern by the same number of nines as numbers it has will suffice. For example:
- 0.5 = 5/9
- 0.62 = 62/99
- 0.264 = 264/999
- 0.6291 = 6291/9999
- 0.05 = 5/90
- 0.000392 = 392/999000
- 0.0012 = 12/9900
- 0.1523 + 0.0000987
- 0.1523 + 987/9990000


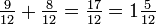


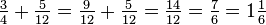


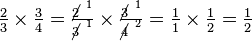


0 komentar:
Posting Komentar