 |
| The Canadarm2 robotic manipulator on the International Space Station is operated by controlling the angles of its joints. Calculating the final position of the astronaut at the end of the arm requires repeated use of trigonometric functions of those angles. |
Trigonometry basics are often taught in school either as a separate course or as part of a precalculus course. The trigonometric functions are pervasive in parts of pure mathematics and applied mathematics such as Fourier analysis and the wave equation, which are in turn essential to many branches of science and technology. Spherical trigonometry studies triangles on spheres, surfaces of constant positive curvature, in elliptic geometry. It is fundamental to astronomy and navigation. Trigonometry on surfaces of negative curvature is part of Hyperbolic geometry.
History
 |
| The first trigonometric table was apparently compiled by Hipparchus, who is now consequently known as "the father of trigonometry." |
Classical Greek mathematicians (such as Euclid and Archimedes) studied the properties of chords and inscribed angles in circles, and proved theorems that are equivalent to modern trigonometric formulae, although they presented them geometrically rather than algebraically. Claudius Ptolemy expanded upon Hipparchus' Chords in a Circle in his Almagest. The modern sine function was first defined in the Surya Siddhanta, and its properties were further documented by the 5th century Indian mathematician and astronomer Aryabhata. These Greek and Indian works were translated and expanded by medieval Islamic mathematicians. By the 10th century, Islamic mathematicians were using all six trigonometric functions, had tabulated their values, and were applying them to problems in spherical geometry. At about the same time, Chinese mathematicians developed trigonometry independently, although it was not a major field of study for them. Knowledge of trigonometric functions and methods reached Europe via Latin translations of the works of Persian and Arabic astronomers such as Al Battani and Nasir al-Din al-Tusi. One of the earliest works on trigonometry by a European mathematician is De Triangulis by the 15th century German mathematician Regiomontanus. Trigonometry was still so little known in 16th century Europe that Nicolaus Copernicus devoted two chapters of De revolutionibus orbium coelestium to explaining its basic concepts.
Driven by the demands of navigation and the growing need for accurate maps of large areas, trigonometry grew into a major branch of mathematics. Bartholomaeus Pitiscus was the first to use the word, publishing his Trigonometria in 1595. Gemma Frisius described for the first time the method of triangulation still used today in surveying. It was Leonhard Euler who fully incorporated complex numbers into trigonometry. The works of James Gregory in the 17th century and Colin Maclaurin in the 18th century were influential in the development of trigonometric series. Also in the 18th century, Brook Taylor defined the general Taylor series.
Overview
 |
| In this right triangle: sin A = a/c; cos A = b/c; tan A = a/b. |
- Sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
- Cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.
- Tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.
The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec), and cotangent (cot), respectively:
With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and their included angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since every polygon may be described as a finite combination of triangles.
Extending the definitions
 |
| Fig. 1a - Sine and cosine of an angle θ defined using the unit circle. |
The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from calculus and infinite series. With these definitions the trigonometric functions can be defined for complex numbers. The complex exponential function is particularly useful.
-

Graphing process of y = sin(x) using a unit circle. -

Graphing process of y = tan(x) using a unit circle. -

Graphing process of y = csc(x) using a unit circle.
Mnemonics
A common use of mnemonics is to remember facts and relationships in trigonometry. For example, the sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters. For instance, a mnemonic for English speakers is SOH-CAH-TOA:- Sine = Opposite ÷ Hypotenuse
- Cosine = Adjacent ÷ Hypotenuse
- Tangent = Opposite ÷ Adjacent
Calculating trigonometric functions
Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions. Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan, and sometimescis and their inverses. Most allow a choice of angle measurement methods: degrees, radians and, sometimes, grad. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers have built-in instructions for calculating trigonometric functions.Applications of trigonometry
 |
| Sextants are used to measure the angle of the sun or stars with respect to the horizon. Using trigonometry and a marine chronometer, the position of the ship can be determined from such measurements. |
Standard identities
Identities are those equations that hold true for any value.Angle transformation formulas
Common formulas
 |
| Triangle with sides a,b,c and respectively opposite angles A,B,C |
In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.
Law of sines
The law of sines (also known as the "sine rule") for an arbitrary triangle states: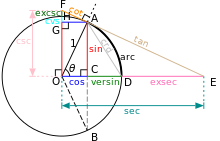 |
| All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O. |
Law of cosines
The law of cosines (known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:Law of tangents
The law of tangents:Euler's formula
Euler's formula, which states that , produces the following analytical identities for sine, cosine, and tangent in terms of e and the imaginary unit i:
, produces the following analytical identities for sine, cosine, and tangent in terms of e and the imaginary unit i:



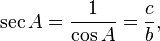










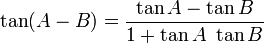
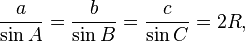
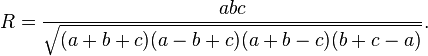
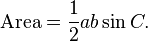
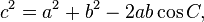

![\frac{a-b}{a+b}=\frac{\tan\left[\tfrac{1}{2}(A-B)\right]}{\tan\left[\tfrac{1}{2}(A+B)\right]}](http://upload.wikimedia.org/math/c/b/5/cb5c755b587d4e4e1f4367c492c4de8d.png)

0 komentar:
Posting Komentar