 |
| Specific elements of a matrix are often denoted by a variable with two subscripts. For instance, a2,1 represents the element at the second row and first column of a matrix A. |
Matrices of the same size can be added or subtracted element by element. The rule for matrix multiplication is more complicated, and two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second. A major application of matrices is to represent linear transformations, that is, generalizations of linear functions such as f(x) = 4x. For example, the rotation of vectors in three dimensional space is a linear transformation. If R is a rotation matrix and v is a column vector (a matrix with only one column) describing the position of a point in space, the product Rv is a column vector describing the position of that point after a rotation. The product of two matrices is a matrix that represents the composition of two linear transformations. Another application of matrices is in the solution of a system of linear equations. If the matrix is square, it is possible to deduce some of its properties by computing its determinant. For example, a square matrix has an inverse if and only if its determinant is not zero. Eigenvalues and eigenvectors provide insight into the geometry of linear transformations.
Matrices find applications in most scientific fields. In every branch of physics, including classical mechanics, optics, electromagnetism, quantum mechanics, and quantum electrodynamics, they are used to study physical phenomena, such as the motion of rigid bodies. In computer graphics, they are used to project a 3-dimensional image onto a 2-dimensional screen. In probability theory and statistics, stochastic matrices are used to describe sets of probabilities; for instance, they are used within the PageRank algorithm that ranks the pages in a Google search. Matrix calculus generalizes classical analytical notions such as derivatives and exponentials to higher dimensions.
A major branch of numerical analysis is devoted to the development of efficient algorithms for matrix computations, a subject that is centuries old and is today an expanding area of research. Matrix decomposition methods simplify computations, both theoretically and practically. Algorithms that are tailored to the structure of particular matrix structures, e.g. sparse matrices and near-diagonal matrices, expedite computations in finite element method and other computations. Infinite matrices occur in planetary theory and in atomic theory. A simple example is the matrix representing the derivative operator, which acts on the Taylor series of a function.
Definition
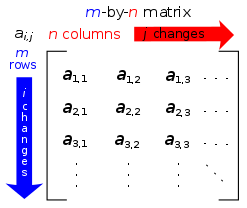
A matrix is a rectangular arrangement of mathematical expressions that can be simply numbers.Commonly the m components of the matrix are written in a rectangular arrangement in the form of a column of m rows:
The horizontal and vertical lines in a matrix are called rows and columns, respectively. The numbers in the matrix are called its entries or its elements. To specify the size of a matrix, a matrix with m rows and n columns is called an m-by-n matrix or m × n matrix, while m and n are called its dimensions. The above is a 4-by-3 matrix.
A matrix with one row (a 1 × n matrix) is called a row vector, and a matrix with one column (an m × 1 matrix) is called a column vector. Any row or column of a matrix determines a row or column vector, obtained by removing all other rows or columns respectively from the matrix. For example, the row vector for the third row of the above matrix A is
Most of this article focuses on real and complex matrices, i.e., matrices whose elements are real or complex numbers, respectively. More general types of entries are discussed below.
Notation
The specifics of matrices notation varies widely, with some prevailing trends. Matrices are usually denoted using upper-case letters, while the corresponding lower-case letters, with two subscript indices, represent the entries. In addition to using upper-case letters to symbolize matrices, many authors use a special typographical style, commonly boldface upright (non-italic), to further distinguish matrices from other mathematical objects. An alternative notation involves the use of a double-underline with the variable name, with or without boldface style, (e.g., ).
).The entry in the i-th row and the j-th column of a matrix is typically referred to as the i,j, (i,j), or (i,j)th entry of the matrix. For example, the (1,3) entry of the above matrix A is 5. The (i, j)th entry of a matrix A is most commonly written as ai,j. Alternative notations for that entry are A[i,j] or Ai,j.
Sometimes a matrix is referred to by giving a formula for its (i,j)th entry, often with double parenthesis around the formula for the entry, for example, if the (i,j)th entry of A were given by aij, A would be denoted ((aij)).
An asterisk is commonly used to refer to whole rows or columns in a matrix. For example, ai,∗ refers to the ith row of A, and a∗,j refers to the jth column of A. The set of all m-by-n matrices is denoted
 (m, n).
(m, n).A common shorthand is
- A = [ai,j]i = 1,...,m; j = 1,...,n or more briefly A = [ai,j]m×n
Some programming languages start the numbering of rows and columns at zero, in which case the entries of an m-by-n matrix are indexed by 0 ≤ i ≤ m − 1 and 0 ≤ j ≤ n − 1. This article follows the more common convention in mathematical writing where enumeration starts from 1.
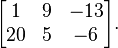


0 komentar:
Posting Komentar